My younger daughter Lottie is 16 today, and I gave her a square card with \(2^4\) on one side and \(4^2\) on the other.

\[2^4 = 4^2\]

This is the only solution to \(a^b = b^a\) for whole numbers \(a\) and \(b\). The proof of this statement is especially elegant. I can't remember where I read it first, but it was when I was doing my A-levels.

Starting with \[a^b = b^a\] taking (natural) logs \[b \log a = a \log b\] and rearranging, we get \[\frac{\log a}{a} = \frac{\log b}{b}\]

Now consider the graph \[y = \frac{\log x}{x}\]

plotted here in red (thanks to Desmos):

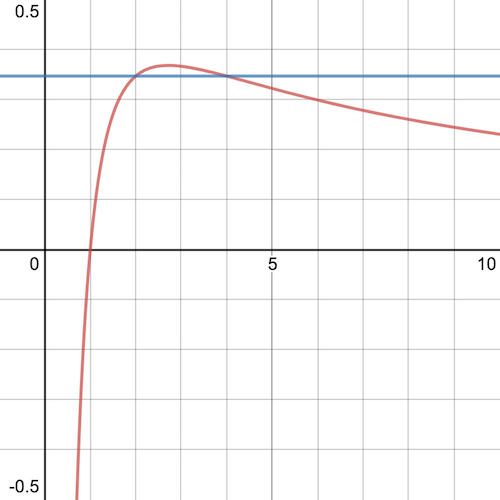
Graph of y = log(x)/x

The notable thing about the graph is that it intercepts the \(x\) axis at \(x=1\), rises to a maximum between \(x=2\) and \(x=3\), then steadily decreases as \(x\) increases, but never reaches the \(x\) axis.

The blue line shows the solution above graphically, since \[\frac{\log 2}{2} = \frac{\log 4}{4} \approx 0.35\]

Now, this graph shows that \(a=2\), \(b=4\) is the only solution.

To see why, imagine that there is another solution, \(a>4\). Then, draw a horizontal line through the point on the graph where \(x=a\), shown here in green:

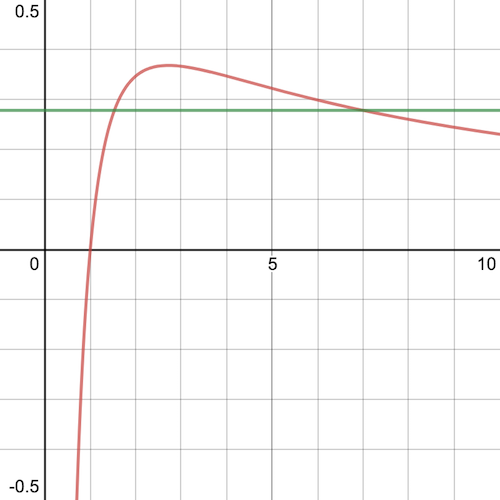
Graph of y = log(x)/x with non-solution

The green line intercepts the red curve strictly between \(x=1\) and \(x=2\), which shows that \(x\) is not a whole number. Therefore, there are no whole number solutions for \(a>4\).

Finally, we can see that \(a=3\) does not have any solutions, for the same reason (the other intercept is strictly between \(x=2\) and \(x=3\) and again is not a whole number).

The thing I like about this proof is that it proves something about whole numbers, by operating in the domain of real numbers, and by using simple arguments about the properties of the graph of a function.

[One last pleasing thing. It's easy to show (by differentiation and setting to zero), that the curve is at its maximum at \(x=e\).]