The Earth Moon Game
If the Moon were the size of a tennis ball then the Earth would be the size of a basketball. How far apart should the balls be placed so that the distance is to scale?
Before you read on, you might like to have a go yourself. If you don't have a tennis ball and basketball to hand, you can play with this online version I wrote.
My kids and I had a stall at our school fair this Friday where we played this as a game:
The Earth's diameter is 12,742 km and the Moon's is 3,475 km, so the Earth's diameter is about 3.7 larger. (We measured the basketball's diameter to be 23.5 cm, and the tennis ball to be 6.5 cm, so the ratio is about 3.6, which is pretty close!)
The Moon is (on average) 384,400 km from the Earth (the Lunar distance, measured from the centres of the two bodies), which is 111 times the Moon's diameter. Scaling this to the tennis ball, we get a distance of 111 × 6.5 cm = 7.2 metres.
Here's a picture showing the results at the end of the fair:
The basketball representing the Earth is in the bottom of the picture, and the tennis ball just visible at the top is the Moon, 7.2 metres away. To the right of the green tape are white flags that are the players' guesses for where the Moon would be.
It's striking that all the guesses were too low. This seems to be a mixture of two things. Firstly, people really do think that the Moon is closer than it actually is. Secondly, people tend to copy other people, so they would place their flags close to where the others were. (We told everyone that the Moon didn't have to be restricted to the green tape - that just happened to be how long it was.)
We saw a few interesting tactics though. One girl put one flag so it was the closest to the Earth compared to all the other flags, then another so it was the furthest out. She seemed to think that everyone else had either over- or underestimated the distance - which of course they had! (She didn't win though, as someone put their flag even further out later on.) Someone else put five flags over a range of about 25cm where she thought the Moon would be.
The most successful approach seemed to be for the player to stand where the Earth is, and have someone walk away holding the tennis ball until it subtends the same angle as the Moon does in the sky (or your mind's eye). This is easier said than done, however. The player in fourth place (who was about five years old) used this technique.
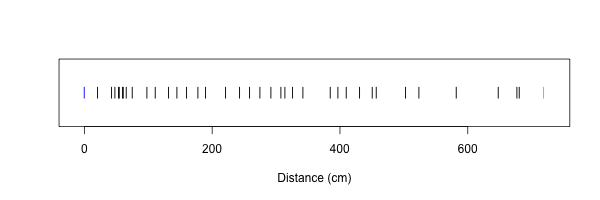
Here's the data plotted graphically, with each flag shown as a line. The blue line represents Earth, and the orange line the Moon.
Interestingly, the guesses did not benefit from the Wisdom of Crowds effect, where the average tends to be a good predictor of the actual answer:
Before you read on, you might like to have a go yourself. If you don't have a tennis ball and basketball to hand, you can play with this online version I wrote.
My kids and I had a stall at our school fair this Friday where we played this as a game:
The Earth's diameter is 12,742 km and the Moon's is 3,475 km, so the Earth's diameter is about 3.7 larger. (We measured the basketball's diameter to be 23.5 cm, and the tennis ball to be 6.5 cm, so the ratio is about 3.6, which is pretty close!)
The Moon is (on average) 384,400 km from the Earth (the Lunar distance, measured from the centres of the two bodies), which is 111 times the Moon's diameter. Scaling this to the tennis ball, we get a distance of 111 × 6.5 cm = 7.2 metres.
Here's a picture showing the results at the end of the fair:
The basketball representing the Earth is in the bottom of the picture, and the tennis ball just visible at the top is the Moon, 7.2 metres away. To the right of the green tape are white flags that are the players' guesses for where the Moon would be.
It's striking that all the guesses were too low. This seems to be a mixture of two things. Firstly, people really do think that the Moon is closer than it actually is. Secondly, people tend to copy other people, so they would place their flags close to where the others were. (We told everyone that the Moon didn't have to be restricted to the green tape - that just happened to be how long it was.)
We saw a few interesting tactics though. One girl put one flag so it was the closest to the Earth compared to all the other flags, then another so it was the furthest out. She seemed to think that everyone else had either over- or underestimated the distance - which of course they had! (She didn't win though, as someone put their flag even further out later on.) Someone else put five flags over a range of about 25cm where she thought the Moon would be.
The most successful approach seemed to be for the player to stand where the Earth is, and have someone walk away holding the tennis ball until it subtends the same angle as the Moon does in the sky (or your mind's eye). This is easier said than done, however. The player in fourth place (who was about five years old) used this technique.
Here's the data plotted graphically, with each flag shown as a line. The blue line represents Earth, and the orange line the Moon.
The opening anecdote [of the book of the same name by James Surowiecki] relates Francis Galton's surprise that the crowd at a county fair accurately guessed the weight of an ox when their individual guesses were averagedFor the Earth Moon Game, however, the median distance was 2.6 metres, and the mean was 2.7 metres, which was 2.3 standard deviations (sd=1.96 metres) from the true distance, 7.2 metres.